- Back to Home »
- DETERMINAN
Senin, 23 September 2019
Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atauUntuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b6492567d55ede81657988571966a6ec_l3.png)
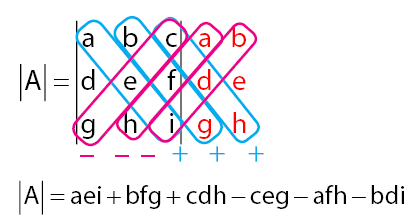
Contoh perhitungan determinan pada matriks ordo 3:
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a8947ae5b1c5dff0a86a995bd7c4f105_l3.png)
![Rendered by QuickLaTeX.com \[ \left| \textrm{A} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ef53da91e11b43e4c90a06150a48d5bd_l3.png)
Selanjutnya, pembahasan kita akan berlanjut ke invers matriks.
- Matriks MinorDiketahui sebuah matriks A dengan ordo 3 seperti terlihat di bawah.
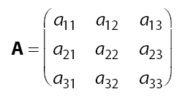
Matriks minor adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan
kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2
seperti persamaan di bawah.
adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan
kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2
seperti persamaan di bawah.

Matriks-matriks minor di atas digunakan untuk mendapatkan matriks kofaktor A.
Kofaktor
Kofaktor baris ke-i dan kolom ke-j disimbolkan dengan

Kofaktor di atas akan digunakan untuk menentukan adjoin matriks yang akan dicari nilai inversnya.
Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
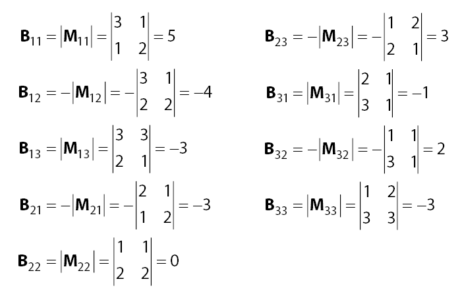
Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.
Tentukan determinan
matriks A = 
Penyelesaian.
Menggunakan
yang diberikan pada Teorema diatas dengan mengambil i = 3 dan j = 1, 2,
dan 3, maka diperoleh.
det(A)
= 
= a31C31 + a32C32
+ a33C33
= a31(-1)3+1M31 + a32(-1)3+2M31
+ a33(-1)3+3M31
= a31M31 – a32M31
+ a33M31
= 3 – 2
– 2 + 2
+ 2
= 3[6(8)-0(6)] – 2[0(8)-8(0)] + 2[0(6)-8(6)]
= 48














