Archive for September 2019
DETERMINAN
Determinan Matriks
Pada Aljabar, determinan matriks dapat diartikan sebagai nilai yang mewakili sebuah matriks bujur sangkar. Simbol nilai determinan matriks A biasanya dinyatakan sebagai det(A) atauUntuk lebih jelasnya, perhatikan cara menghitung determinan di bawah.
Determinan Matriks Ordo 2 x 2
Seperti yang sobat idschool sudah ketahui, matriks ordo 2 dinyatakan seperti bentuk di bawah.
Contoh Soal:
Tentukan nilai determinan matriks
Matriks Ordo 3 adalah matriks bujur sangkar dengan banyaknya kolom dan baris sama dengan tiga. Bentuk umum matriks ordo 3 adalah sebagai berikut.
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b6492567d55ede81657988571966a6ec_l3.png)
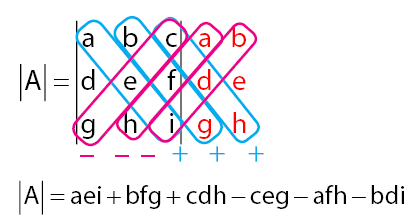
Contoh perhitungan determinan pada matriks ordo 3:
![Rendered by QuickLaTeX.com \[ \textrm{A} \; = \; \begin{bmatrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{bmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-a8947ae5b1c5dff0a86a995bd7c4f105_l3.png)
![Rendered by QuickLaTeX.com \[ \left| \textrm{A} \right| \; = \; \left| \begin{matrix} 1 & 2 & 1 \\ 3 & 3 & 1 \\ 2 & 1 & 2 \end{matrix} \right| \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ef53da91e11b43e4c90a06150a48d5bd_l3.png)
Selanjutnya, pembahasan kita akan berlanjut ke invers matriks.
- Matriks MinorDiketahui sebuah matriks A dengan ordo 3 seperti terlihat di bawah.
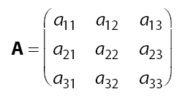
Matriks minor adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan
kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2
seperti persamaan di bawah.
adalah matriks yang diperoleh dengan cara menghilangkan baris ke-i dan
kolom ke-j dari matriks A sehingga diperoleh matriks minor berordo 2
seperti persamaan di bawah.

Matriks-matriks minor di atas digunakan untuk mendapatkan matriks kofaktor A.
Kofaktor
Kofaktor baris ke-i dan kolom ke-j disimbolkan dengan

Kofaktor di atas akan digunakan untuk menentukan adjoin matriks yang akan dicari nilai inversnya.
Menentukan Kofaktor:
Berikut ini adalah hasil perhitungan nilai-nilai kofaktor untuk matriks B. Silahkan lihat kembali bagaimana cara mendapatkan nilai kofaktor pada rumus yang telah dibahas di atas jika belum hafal rumusnya.
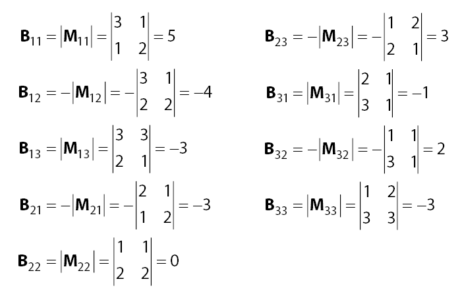
Untuk menentukan invers B, kita membutuhkan matriks adjoin B. Sehingga, kita perlu menentukan matriks adjoin B terlebih dahulu.
Tentukan determinan
matriks A = 
Penyelesaian.
Menggunakan
yang diberikan pada Teorema diatas dengan mengambil i = 3 dan j = 1, 2,
dan 3, maka diperoleh.
det(A)
= 
= a31C31 + a32C32
+ a33C33
= a31(-1)3+1M31 + a32(-1)3+2M31
+ a33(-1)3+3M31
= a31M31 – a32M31
+ a33M31
= 3 – 2
– 2 + 2
+ 2
= 3[6(8)-0(6)] – 2[0(8)-8(0)] + 2[0(6)-8(6)]
= 48
MATRIKS
pengertian matriks dan jenisnya
Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap
Pengertian Matriks - Pelajaran matematika mengenai matriks biasanya diajarkan pada siswa-siswi yang duduk di bangku SMA atau SMK. Materi ini bisa dibilang menyenangkan untuk dipelajari karena untuk memahaminya kita diharuskan untuk memutar otak dan menggunakan logika pemikiran secara maksimal. Sebagai dasar untuk mempelajari materi matriks matematika, pada postingan ini rumus matematika dasar akan menjelaskan kepada kalian mengenai definisi atau pengertian dari matriks matematika serta unsur-unsur yang ada di dalamnya. Sehingga ketika nanti kalian memulai untuk mempelajari perhitungan matematika yang berhubungan dengan matriks, kalian sudah memiliki pengetahuan dasar dan bisa memahami materi pelajaran tersebut dengan lebih baik.Definisi Matriks Matematika dan Jenis-jenis Matriks
Pertama-tama mari kita lihat definisi matriks menurut wikipedia:
"Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks."
Selanjutnya, secara umum matriks dapat diartikan sebagai sebuah
susunan atau kumpulan dari beberapa bilangan yang disusun berdasarkan kepada
baris dan kolom yang bentuknya persegi panjang. Matriks memiliki ciri khas
khusus dimana biasanya bilangan yang menjadi elemen dari sebuah matriks disusun
dengan diapit oleh tanda kurung siku [] namun terkadang ada juga elemen matriks
yang diapit oleh tanda kurung biasa ().
Ukuran dari sebuah matriks disebut dengan ordo yang menjelaskan jumlah
dari kolom dan baris yang ada di dalam matriks tersebut.
Ukuran dari sebuah matriks dapat di simbolkan dengan rumus berikut
ini:
Amxn
A = Nama Matriks
m = jumlah baris
n = jumlah kolom
mxn = ordo matriks
Contoh:
Jangan sampai terbalik dalam membaca ordo matriks, ingatlah bahwa ordo
matriks adalah banyaknya baris dikali dengan banyaknya kolom.
Diagonal utama dan diagonal sekunder pada matriks
Di dalam materi mengenai matriks juga dikenal istilah diagonal. Ada dua
jenis diagonal di dalam matriks yaitu diagonal utama dan diagonal sekunder. Diagonal
utama merupakan garis miring yang ditarik dari sisi kiri atas matriks menuju
sisi kanan bawah matriks. Sementara diagonal sekunder adalah kebalikannya. Seperti
bisa dilihat pada gambar berikut:
Jenis-Jenis Matriks Berdasarkan Banyaknya Baris dan Kolom
Matriks Persegi
Merupakan matriks yang memiliki jumlah baris dan kolom yang sama,
misalnya 4x4, 2x2, atau 5x5. Sehingga ordonya dilambangkan n x n.
Matriks Baris
Adalah matriks yang hanya memiliki satu buah baris namun memiliki
beberapa kolom. Matriks ini ordonya adalah 1
x n dimana n harus lebih besar dari
1. Contohnya 1 x 2, 1 x 4, 1 x 6, dsb.
Matriks kolom
Merupakan kebalikan dari matriks baris. Hanya terdiri dari satu kolom
namun memiliki beberapa baris. Ordo dari matriks ini adalah n x 1 dimana n harus lebih besar dari 1. Contohnya adalah 2 x 1, 3 x 1, 5 x 1,
dsb.
Matriks Mendatar
Adalah matriks yang memiliki jumlah kolom yang lebih banyak
dibandingkan jumlah barisnya. Contohnya adalah 3 x 5, 4 x 6, dsb.
Matriks Tegak
Merupakan kebalikan dari matriks mendatar dimana jumlah barisnya lebih
banyak dibandingkan jumlah kolomnya. Contohnya adalah 6 x 3, 4 x 2, 8 x 5, dsb.
Jenis Matriks Berdasarkan pada Pola Elemennya
Matriks Nol
Merupakan matriks dengan ordo m x n dimana seluruh elemennya memiliki
nilai nol.
Matriks Diagonal
Merupakan matriks persegi yang elemennya bernilai nol kecuali pada
diagonal utamanya.
Matriks Identitas
Adalah matriks yang diagonal utamanya di isi dengan elemen bernilai 1
sementara elemen yang lain nilainya adalah nol.
Matriks Segitiga Atas
Adalah matriks yang keseluruhan nilai dibawah diagonal utamanya adalah
nol.
Matriks Segitiga Bawah
Merupakan kebalikan dari matriks segitiga atas dimana seluruh elemen
yang ada di atas diagonal utamanya bernilai nol.
Matriks Simetris
Merupakan sebuah matriks dimana elemen yang ada di atas dan dibawah
doagonal utamanya memiliki susunan nilai yang sama.
Matriks Skalar
Adalah matriks yang memiliki elemen diagonal utama bernilai sama
sementara elemen yang lain nilainya adalah nol.
Inilah akhir dari Materi Pengertian dan Jenis-jenis Matriks Matematika Lengkap. Semoga dapat mempermudah kalian nantinya ketika memasuki pelajaran matematika yang membahas persoalan matriks.
Tentukan hasil perkalian matriks bilangan A dan B di bawah ini.
![Rendered by QuickLaTeX.com \[ A = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-b23b9fb4d00bd194db9327323f0a11d8_l3.png)
![Rendered by QuickLaTeX.com \[ B = \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-716549d520f95d973b133ba206da3a98_l3.png)
Pembahasan:
![Rendered by QuickLaTeX.com \[ A \times B = \begin{pmatrix} 3 & 4 \\ 1 & 2 \end{pmatrix} \times \begin{pmatrix} 7 & 5 \\ 6 & 4 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-981d0c251d8cb40ff9b109545924741d_l3.png)
![Rendered by QuickLaTeX.com \[ = \begin{pmatrix} 3 \cdot 7 + 4 \cdot 6 & 3 \cdot 5 + 4 \cdot 4 \\ 1 \cdot 7 + 2 \cdot 6 & 1 \cdot 5 + 2 \cdot 4 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-63d9ab10ed180f0adba01091a9b6336d_l3.png)
![Rendered by QuickLaTeX.com \[ = \begin{pmatrix} 21 + 24 & 15 + 16 \\ 7 + 12 & 5 + 8 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-dee37317aba4acbe3661a717885978b5_l3.png)
![Rendered by QuickLaTeX.com \[ = \begin{pmatrix} 45 & 31 \\ 19 & 13 \end{pmatrix} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-26007d912439574ebcd749fbe409ebd4_l3.png)
Perkalian dua buah matriks dengan masing-masing mempunyai ukuran 2 x 2 di atas bisa menghasilkan matriks dengan ukuran 2 x 2 pula. Proses perkalian bilangan dua matriks ini tak begitu rumit. Hal ini dikarenakan tiap anggota penyusun matriks dengan ukuran 2 x 2 hanya ada 4 anggota untuk tiap matriks. Dengan begitu, perkaliannya bisa dengan mudah dilakukan.
Contoh Soal Perkalian Matriks
Berikut adalah beberapa soal perkalian bilangan matriks lengkap dengan pembahasan selengkapnya untuk anda.Tentukan hasil perkalian matriks bilangan A dan B di bawah ini.
Pembahasan:
Perkalian dua buah matriks dengan masing-masing mempunyai ukuran 2 x 2 di atas bisa menghasilkan matriks dengan ukuran 2 x 2 pula. Proses perkalian bilangan dua matriks ini tak begitu rumit. Hal ini dikarenakan tiap anggota penyusun matriks dengan ukuran 2 x 2 hanya ada 4 anggota untuk tiap matriks. Dengan begitu, perkaliannya bisa dengan mudah dilakukan.













